【研究意义】大豆是土地密集型农产品,单产较低,既是重要的粮食作物,也是油料的重要来源,在国民经济中占有重要地位。大豆价格的稳定是大豆市场健康发展的重要前提和保障,但我国人均耕地面积较少,大豆主要依靠进口,易受到国际政治经济、国家宏观政策等因素的影响。因此,了解当前市场价格变化情况并对大豆价格建立有效的预测模型,洞悉未来市场价格的变化趋势,有助于规避风险,对促进大豆市场健康发展具有重要的实际意义。【前人研究进展】目前在大豆价格的研究领域多采用单一模型,如徐鑫洲等[1]基于系统动力学的我国大豆价格预测分析,朱婧等[2]基于改进GM]1,1)模型的中国大豆价格预测。这类单一预测模型对时间序列的波动特征要求较高,对于具有非线性、非平稳特点的大豆时间序列来说,其预测精度有待进一步提高。经验模态分解(Empirical Mode Decomposition,EMD)是Huang等[3]于1998年提出的一种新型自适应信号时频处理方法。与傅里叶分解、小波分解等方法不同,EMD方法是依据信号自身的时间尺度特征来进行信号分解,无需预先选择任何基函数,在处理非平稳及非线性信号上,具有非常明显的优势。国内一些学者已经将EMD运用于预测领域,如叶林等[4]基于经验模态分解和支持向量机的短期风电功率组合预测模型,王文波等[5]基于EMD与神经网络的中国股票市场预测,蒋轶军等[6]基于EEMD和进化KPCR的复杂时间序列自适应预测模型,均取得了良好的预测效果。上述分解集成的思想,能有效解决单一预测模型的不足。【本研究切入点】基于这种思想,本研究考虑大豆时间序列在实际分解过程中存在模态混淆和端点效应问题,对EMD分解方法进行了改进,在分量预测模型SVR的建立过程中,通过遗传算法实现模型参数的优化选择。【拟解决的关键问题】将不同分量的预测结果集成,实现准确预测,对于指导大豆的生产和进出口贸易具有较高的指导意义。
1 材料与方法
1.1 EEMD分解优化
1.1.1 集成经验模态分解 EMD方法本质上是对信号进行平稳化处理,将信号中真实存在的不同尺度波动或趋势逐级分解出来,产生一系列具有不同特征尺度的数据序列,每一个序列成为一个本征模态函数(Intrinsic Mode Function,IMF)。最低频率的IMF分量称为残余项,代表了原始信号的趋势或均值,分解得到的各个IMF突出了数据的局部特征并具有明显的物理意义。
为了改善EMD中存在的模态混叠现象,Wu等[7]进一步提出了EEMD方法。该方法是一种新的噪声辅助数据分析方法,其核心思想是认为每个观察到的数据都融合了实际的时间序列信息和噪声,因此即使同一过程数据被不同的人收集得到,也具有不同的噪声水平,但是其整体均值接近于真实的时间序列。为解析出数据的真实信号,将多组具有有限振幅的白噪声序列添加到原始序列上,然后分别进行分解,将相应分量的均值作为真实分量。EEMD方法的步骤如下:
(1)将正态分布的白噪声n(t)加到原始信号X(t),计算新的信号:
(2)将新的信号X(t)进行EMD分解,得到各分量imfi(t)和残余项r(t)。
(3)重复N次步骤(1)和(2),每次加入不同的正态分布白噪声序列:
(4)将每次得到的imf分量和残余项r(t)做集成平均处理后作为最终结果:

1.1.2 平行延拓法 端点效应是Hung等[3]在研究EMD的筛分过程时发现的,指的是在EMD分解中反复运用3次样条方法根据极值点对上、下包络进行插值,但信号的端点不可能同时是极大值点或极小值点,因此得到的包络曲线会在两侧的端点附近出现幅值发散的现象,随着筛分过程的不断进行,发散现象逐渐传播至内,使分解结果严重失真,产生假频信号。
平行延拓法是一种基于极值点的延拓方法,它通过利用端点附近的两个相邻极值点(一个极大值、一个极小值)处斜率相等这一特性,来获取被分析的有限信号序列左、右两端的延拓极值点,可以有效解决EMD中的端点效应问题[8]。
假设被分析信号序列{(t(n),Z(n))|n=1,2,…,},其极大值信号序列为{ (tm(i),Z(i))|i=1,2,…,Nmax},极小值信号序列为 {(tn(i),V( i))|i=1 ,2,…,Nmin},并假设信号序列的起始极值点为1个极小值点,信号序列最末端的极值点为极大值点,平行延拓法的计算步骤如下:
(1)把起始端点作为起始延拓的极大值点,获取极大值点值为:
(2)获得起始端点相邻极值点连线的斜率:
(3)求取起始延拓的极小值点值为:
(4)求取起始延拓的极值点横坐标为:
(5)与被分析信号的起始端相同,把终止端点作为末端延拓的极小值点,获取极小值点值为:
(6)获得信号序列终止端点的相邻极值连线的斜率:
(7)求取末端延拓的极大值点值为:
(8)求取末端延拓的极值点横坐标:
通过平行延拓方法在原始时间序列两端延拓出极大值和极小值,避免了直接将端点作为极值点进行分解的鲁棒性,可以抑制端点效应带来的问题,有效改善原始EMD方法的分解效果。
1.2 基于改进的EEMD和SVR的预测建模
以上述理论为基础,我们提出一种优化模型,对EMD模型进行优化分解,得到最佳的分解分量,以实现更精确的预测结果。基于改进的EEMD和支持向量回归的预测建模过程如图1所示,对于给定的时间序列数据,预测建模过程的具体实现步骤如下[9-10]:
(1)以原始时间序列为对象,加入白噪声序列,得到新的序列X(t)。
(2)对新的时间序列X(t)进行端点处理,采用平行延拓法对序列两端延拓,重构出极大值和极小值,再对延拓后的序列X(t)*进行EMD分解,得到多个模式分量imfi(t)。
(3)重复步骤(1)和(2),但是添加不同的白噪声,将每次得到的多个模式分量和残余项相应进行集成平均作为最终的分量![]() 和残余项r*(t)。
和残余项r*(t)。
(4)对每个分量建立SVR模型,采用遗传算法对模型参数进行优化,得到不同分量模型相应的参数,进而得到不同分量的最佳的序列预测模型:
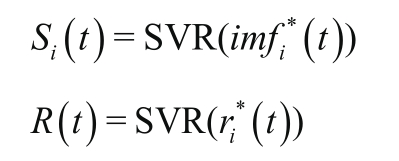
(5)在各个分量预测结果的基础上,集成得到最终的时间序列预测值Y(t):
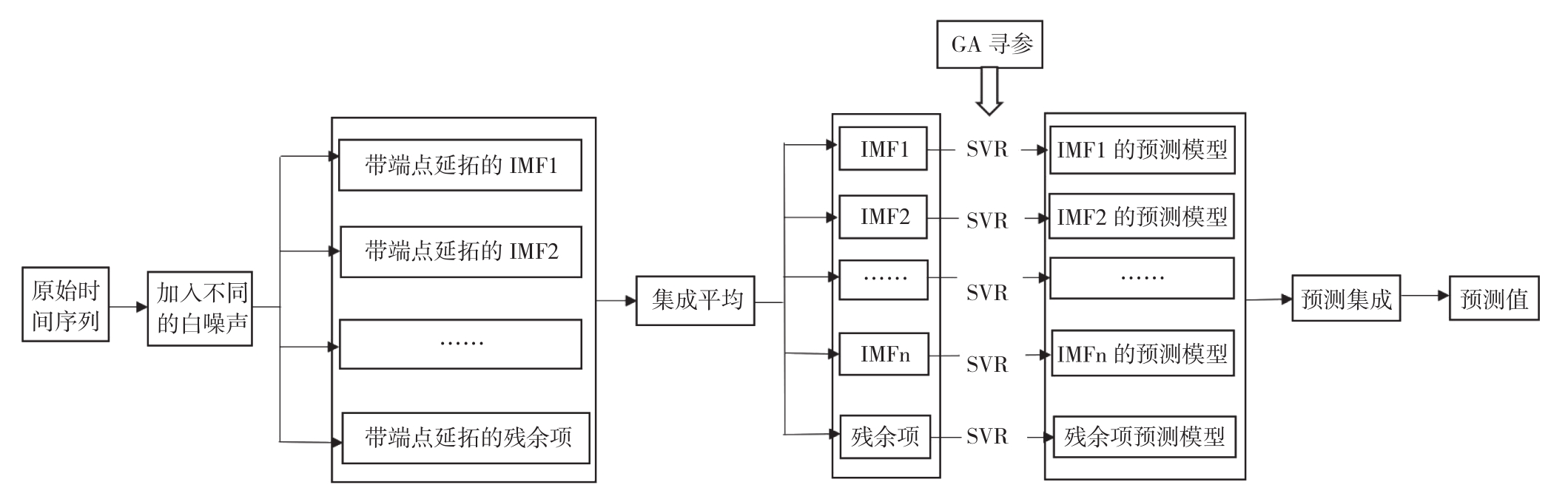
图1 基于改进的EEMD和支持向量回归(SVR)的建模过程
Fig.1 Modeling process based on improved EEMD and support vector regression (SVR)
1.3 数据获取
选用中国集贸市场大豆—中等月度价格展开研究。以2000年1月至2018年10月共226个月度价格数据为数据集,选取2000年1月至2015年1月共181个数据作为训练集,2015年2月—2018年10月共45个数据作为测试集,具体数据均来源于中国经济与社会发展统计数据库(图2)。

图2 全国集贸市场大豆价格(元/kg)
Fig.2 Soybean prices in Chinese market(yuan/kg)
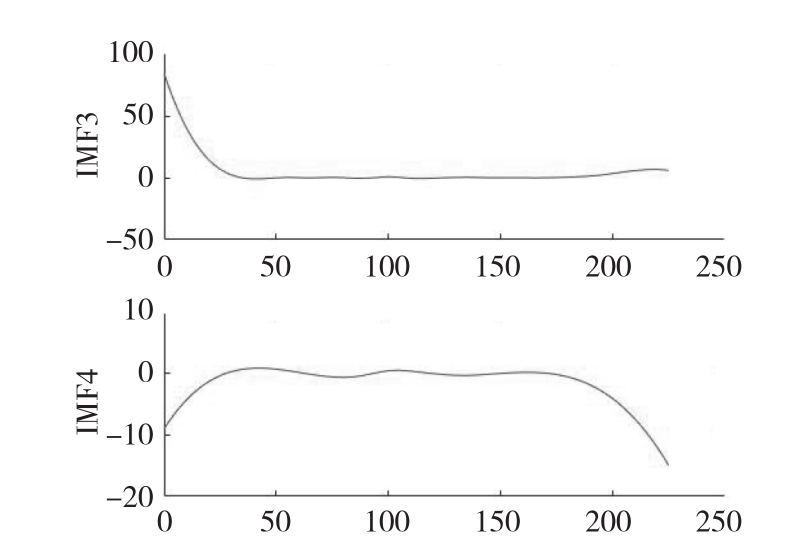
图3 EMD分解IMF3和IMF4
Fig.3 IMF3 and IMF4 decomposed by EMD
2 结果与分析
2.1 价格序列分解与分析
为验证平行延拓端点处理方法的优化效果,采用EMD分别对中国集贸市场大豆—中等月度价格序列进行分解,得到的IMF3和IMF4分量如图3所示;对中国集贸市场大豆—中等月度价格序列平行延拓后再进行EMD分解,得到的IMF3和IMF4分量如图4所示。对比图3和图4可以看出,原始EMD分解的序列体现出明显的端点效应,而该现象经过平行延拓法处理后可以得到有效抑制。
采用EEMD分解中国集贸市场大豆—中等月度价格序列,设置Nstd=0.01,NE=100,较好的解决了模态混叠的问题,得到的分量图和频谱图如图5和图6所示。通过改进分解方法得到5个分量和残余项,从频谱图可看出经过该优化模型分解得出的IMF分量没有明显的模态混叠现象。其中,IMF1~IMF3频率较高,代表短期内不平衡的现象,该现象发生频繁,但影响时长小;IMF4和IMF5分量频率较低,代表大豆价格短期内重大事件对市场价格的影响[11],影响时长相对较大;残余项则代表大豆价格长期的发展趋势,和国家的经济发展趋势一致,稳步上升。
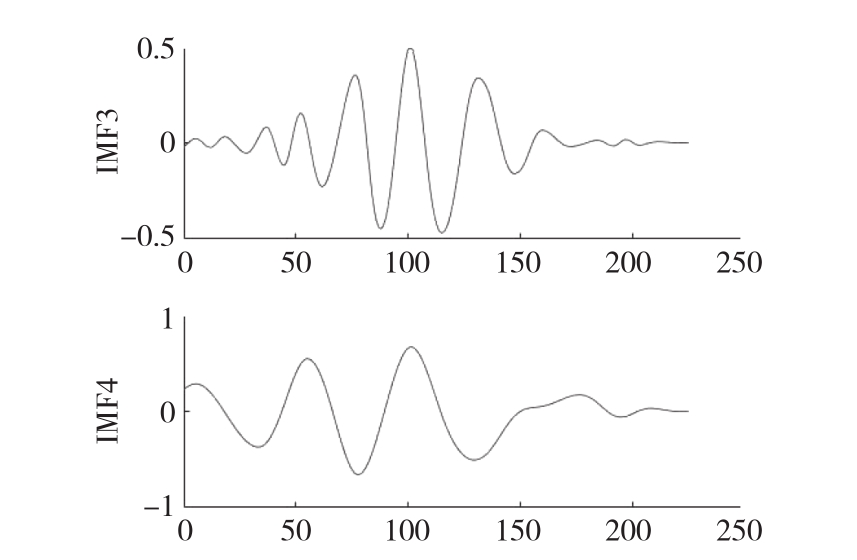
图4 平行延拓IMF3和IMF4分量
Fig.4 Parallel extension components-IMF3 and IMF4
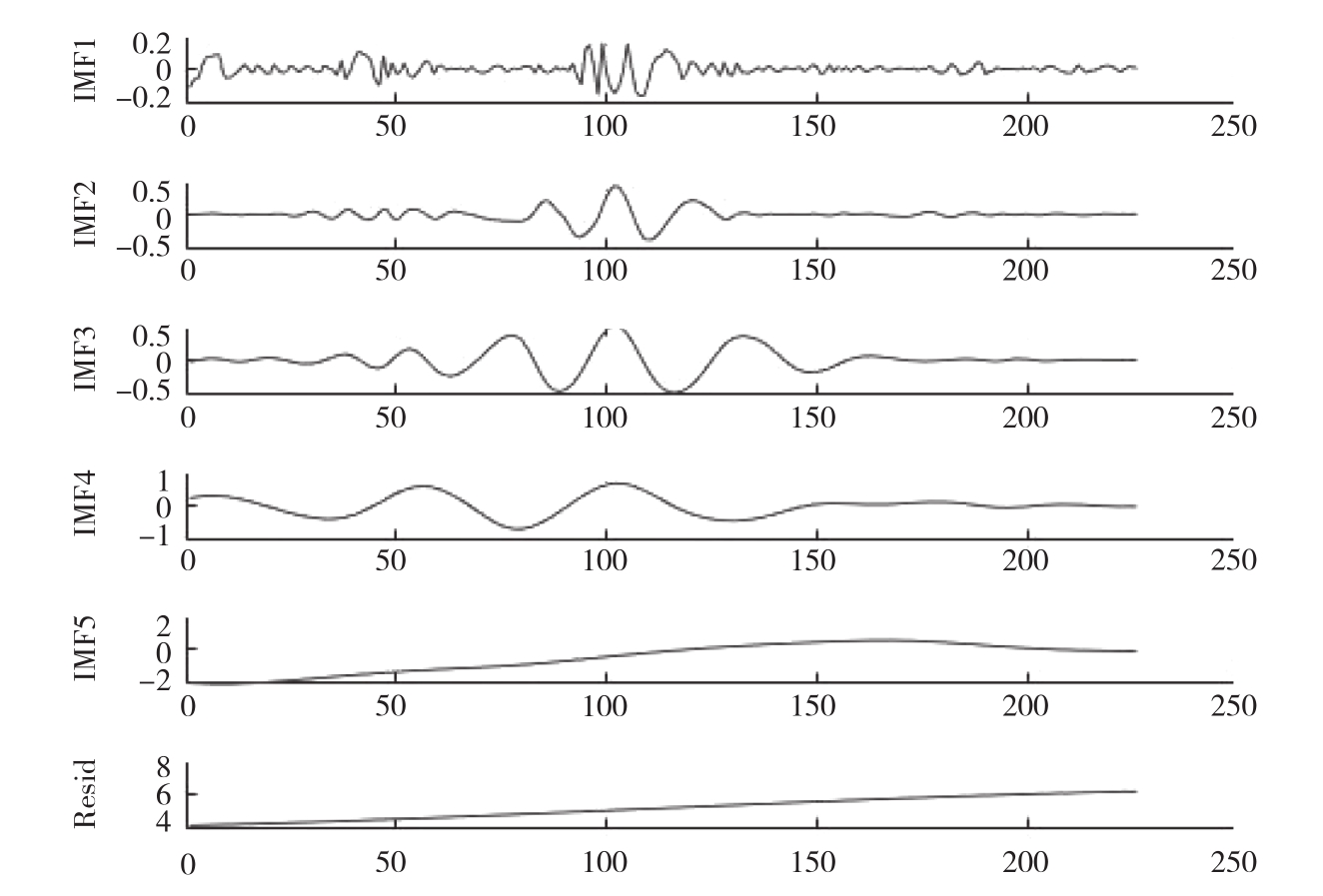
图5 EEMD和平行延拓优化的价格序列分解
Fig.5 Price sequence decomposition of EEMD and parallel extension optimization
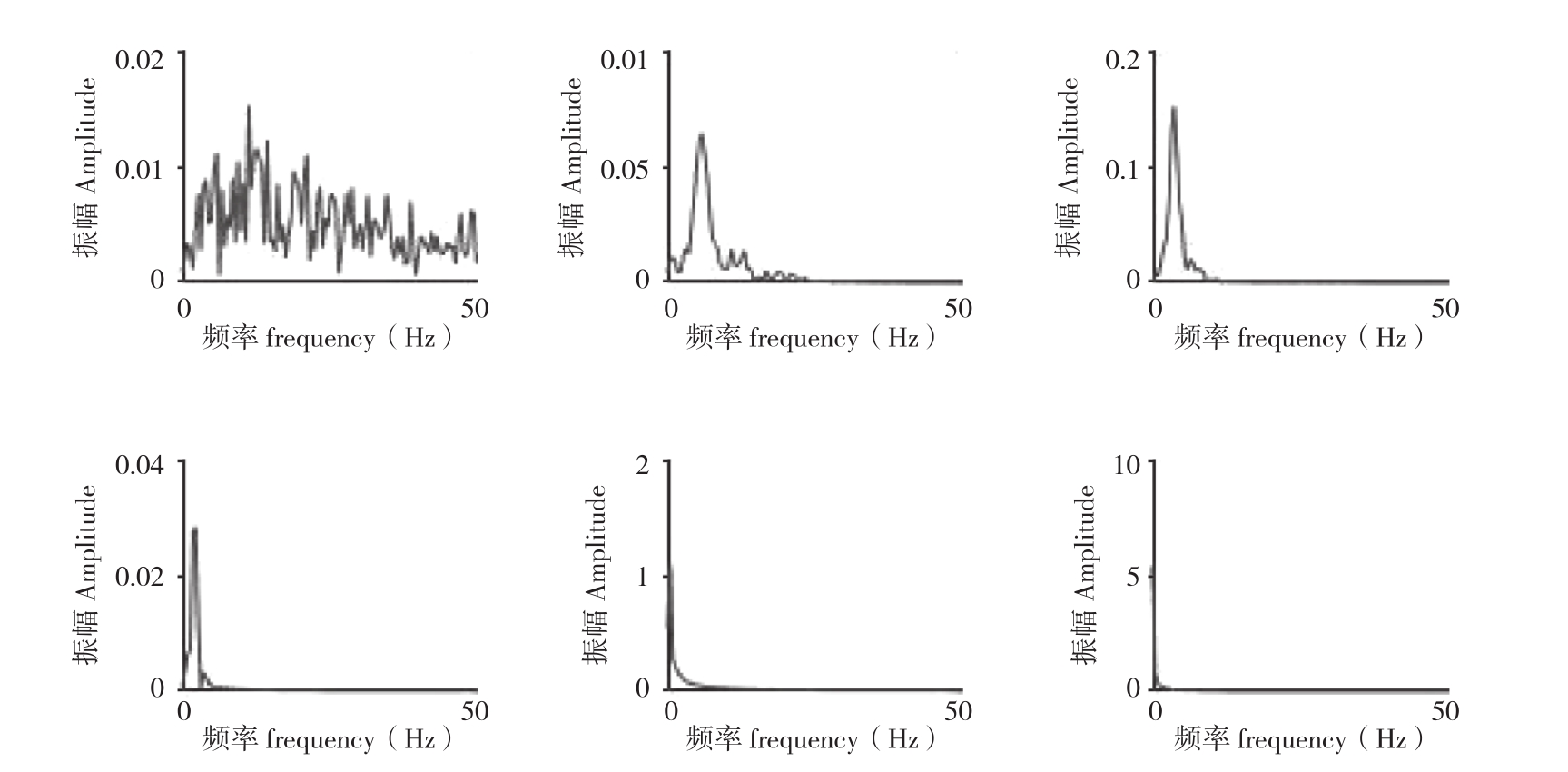
图6 EEMD和平行延拓优化分解频谱图
Fig.6 EEMD and parallel extension optimization decomposition spectrum
2.2 SVR预测模型构建
通过改进的EEMD算法得到6个平稳分量,使用SVR预测模型,代入遗传算法寻得的参数,对各分量进行分别预测并将预测值进行集成得到预测价格。
遗传算法运行中,设置参数迭代次数最大为100次,惩罚因子、核参数的边界设置均为[0,100],遗传算法默认适应度函数值越大即代表寻找参数为最优,本研究选用均方误差MSE的倒数作为适应度函数,作为迭代寻优的标准,具体形式为:
式中,yi(i=1,2,3,....n)为模型预测值,Yi(i=1,2,3,....n)为实际数值,n为数据点的个数,最终得到模型的最优参数。
2.3 预测结果与分析
为了衡量所提出方法的有效性,分别采用MSE、均方根误差(Root Mean Square Error,RMSE)以及平均百分比误差(Mean Absolute Percentage Error,MAPE)3种常用的误差指标评价模型的预测精度,具体描述形式如下:
(1)均方误差:见2.2公式
(2)均方根误差
(3)平均百分比误差
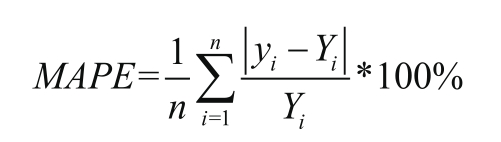
式中,yi(i=1,2,3,....n)为模型预测值,Yi(i=1,2,3,....n)为实际数值,n为样本数量。
为了评价所提出模型的预测效果,选用无端点延拓EMD、端点作为极值点EMD、平行延拓后EMD、平行延拓后EEMD 4种分解方法和原始价格数据直接预测5种模型,将预测结果进行分析比较,在3种预测评价指标下的具体结果见表1。从表1可以看出,平行延拓后EEMD分解模型的预测精度相对其他方法有较大提高,普遍高于原价格直接预测、无端点延拓EMD和把端点作为极值点EMD 3种预测模型,相比于平行延拓EMD模型也有较好的预测效果,体现出更好的预测性能。
表1 模型预测性能比较
Table 1 Comparison of different model prediction performance

模型Model MSE RMSE MAPE直接预测Direct prediction 0.03 0.17 2.41无端点延拓EMD Unprovoked point extension EMD 4.41 2.10 32.78端点作为极值点EMD Endpoint as extreme point EMD 0.05 0.23 3.36平行延拓EMD Parallel extension EMD 0.02 0.14 1.52平行延拓EEMD Parallel extension EEMD 0.0026 0.05 0.70
5种预测模型的效果如图7和图8所示。通过预测图我们可直观发现平行延拓后EEMD模型的预测效果和真实值相近,而其余几种处理方法都有较大误差。

图7 无端点延拓EMD预测结果
Fig.7 EMD prediction of unprovoked point extension
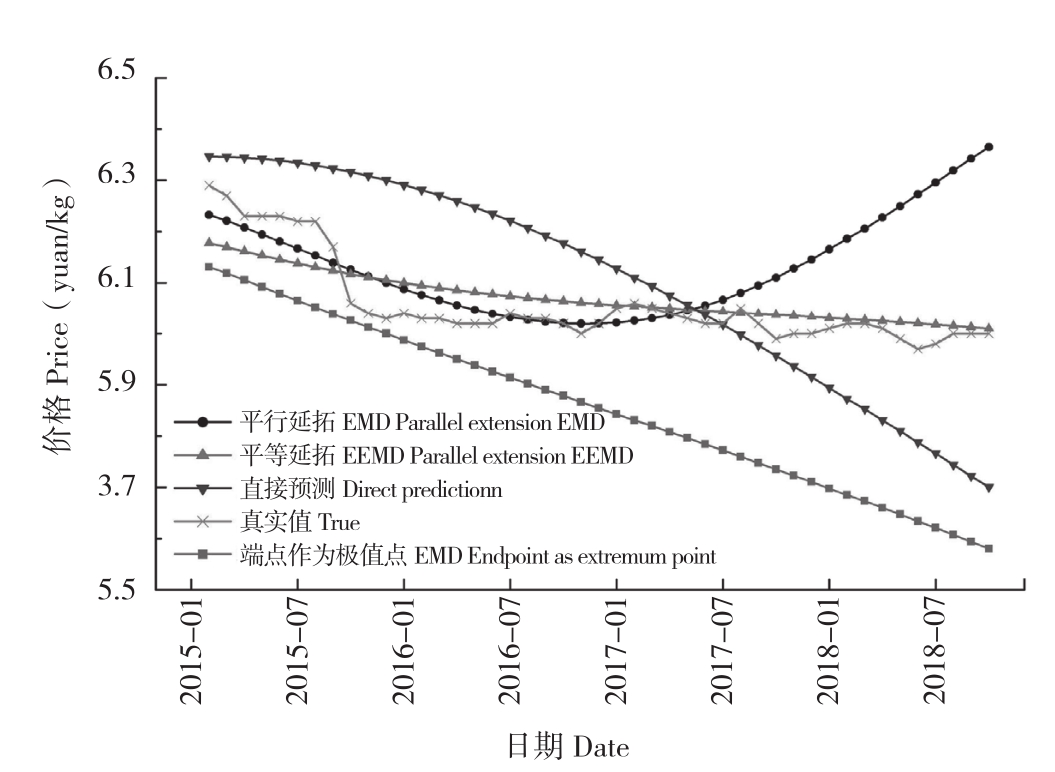
图8 其余4种模型预测结果
Fig.8 Prediction result of the remaining four models
3 讨论
本研究考虑大豆时间序列在实际分解过程中存在模态混淆和端点效应问题,对EMD分解方法进行了改进,在分量预测模型SVR的建立过程中,通过遗传算法实现模型参数的优化选择,将不同分量的预测结果集成,以实现准确预测,对于指导大豆的生产和进出口贸易具有较高的指导意义:(1)经过平行延拓后的EMD算法相对于直接EMD预测的效果更好,通过对序列两端进行延拓,构造出新的极值点再进行分解,有效抑制了EMD分解中存在的端点效应问题[12]。(2)EEMD有针对性地引入白噪声,有效解决了模态混叠问题,通过EEMD得到不同的分解序列,与传统预测方法相比,可以得到平稳的时间序列,对每个分量用以相应的具体模型,不同的参数选择可以得到更为精准的预测效果[13-15]。(3)相对于平行延拓EMD分解,通过平行延拓出极值点再进行EEMD分解,得到的分解序列预测效果更好、精度更高,可以同时抑制模态混叠和端点效应造成的影响[16]。(4)遗传算传通过把问题解的组成空间映射为遗传空间,把可能的解编码成一个向量即染色体,通过不断计算各染色体的适应值,选择最好的染色体,从而获得最优解,通过引入遗传算法优化SVR模型的惩罚因子和核参数,能够较好解决预测模型中的参数优选问题,有效优化预测模型[17-19]。
4 结论
本研究将EMD信号分解处理的方法运用到大豆价格预测中,将原本非平稳、非线性的数据分解为若干平稳数据分量和残余项,通过添加白噪声和对原始时间序列进行平行延拓的处理方法,有效地解决了模态混叠和端点效应问题,对每一个 IMF 分量分别用不同的支持向量机模型,并对其通过遗传算法单独选择最优的核函数和参数,再进行集成预测,相对于传统的预测算法,提高了大豆预测精度。
[1]徐鑫洲,马开平.基于系统动力学的我国大豆价格预测分析[J].大豆科学,2018,37(5):787-793.doi: 10.11861/j.is sn.1000-9841.2018.05.0787.XU X Z, MA K P.Prediction and analysis of soybean price in China based on system dynamics[J].Soybean Science, 2018,37(5):787-793.doi:10.11861/j.issn.1000-9841.2018.05.0787.
[2]朱婧,范亚东,徐勇.基于改进 GM(1,1)模型的中国大豆价格预测[J].大豆科学,2016,35(2):315-319.doi:10.11861/j.issn.1000-9841.2016.02-0315.ZHU J, FAN Y D, XU Y.Soybean price prediction in China based on modified GM(1, 1)Model[J].Soybean Science, 2016,35(2):315-319.doi:10.11861/j.issn.1000-9841.2016.02-0315.
[3]HUANG N E, SHEN Z, LONG S R.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society of London Serices,1998,459: 2317-2345.doi:10.1098/rspa.1998.0193.
[4]叶林,刘鹏.基于经验模态分解和支持向量机的短期风电功率组合预测模型[J].中国电机工程学报,2 011,31(31):102-108.doi:10.13334/j.0258-8013.pcsee.2011.31.014.YE L, LIU P.Short-term wind power combination forecasting model based on empirical mode decomposition and support vector machine[J].Proceedings of the CSEE, 2011,31(31):102-108.doi:10.13334/j.0258-8013.pcsee.2011.31.014.
[5]王文波,费浦生,羿旭明.基于EMD与神经网络的中国股票市场预测[J].系统工程理论与实践,2010,30(6):1027-1033.doi:10.12011/1000-6788(2010)6-1027.WANG W B, FEI P S, YI X M.China stock market forecast based on EMD and neural network[J].Systems Engineering-Thero &Practice, 2010,30(6):1027-1033.doi:10.12011/1000-6788(2010)6-1027.
[6]蒋铁军,张怀强,王先甲.基于EEMD和进化KPCR的复杂时间序列自适应预测建模[J].系统工程理论与实践,2014,34(10):2722-2730.doi:10.12011/1000-6788(2014)10-2722.JIANG Y J,ZHANG H Q,WANG X J.Complex time series adaptive prediction modeling based on EEMD and evolutionary KPCR[J].Systems Engineering-Thero&Practice, 2014,34(10):2722-2730.doi:10.12011/1000-6788(2014)10-2722.
[7]WU Z, HUANG N E.Ensemble empirical mode decomposition: a noise assisted data analysis method[J].Advances in Adaptive Data Analysis, 2009,1(1):1-41.:
[8]茆美琴,龚文剑,张榴晨,曹雨,徐海波.基于EEMD-SVM方法的光伏电站短期出力预测[J].中国电机工程学报,2013,33(34):17-24,5.doi:10.13334/j.0258-8013.pcsee.2013.34.007.MAO M Q, GONG W J, ZHANG L C, CAO Y, XU H B.Short-term photovoltaic generation forecasting based on EEMD-SVM combined method[J].Proceedings of The CSEE, 2013,33(34):17-24,5.doi:10.13334/j.0258-8013.pcsee.2013.34.007.
[9]邸浩,赵学军,张自力.基于EEMD-LSTM-Adaboost的商品价格预测[J].统计与决策,2018,34(13):72-76.doi: 10.13546/j.cnki.tjyjc.2018.13.016.DI H, ZHAO X J, ZHANG Z L.Commodity price forecast based on EEMD-LSTM-Adaboost[J].Control and Decision,2018,34(13):72-76.doi: 10.13546/j.cnki.tjyjc.2018.13.016.
[10]YUSUF Y, BAHADIR B.Empirical mode decomposition bases denoising method with support vector regression for series prediction:A case study for electricity load forecasting[J].Measurement, 2017(103): 52-61.
[11]刘力宇.中美贸易战下国际大豆价格波动、影响及中国策略[J].价格月刊,2019(1):23-26.doi: 10.14076/j.issn.1006-2025.2019.01.04.LIU L Y.International soybean price fluctuation, impact and China strategy under Sino-US trade war[J].Prices Monthly, 2019(1):23-26.doi:10.14076/j.issn.1006-2025.2019.01.04.
[12]管志威,陈国初,徐余法,俞金寿.基于改进EMD与SVM的风电功率短期预测模型[J].控制工程,2014,21(6):833-837.doi:10.14107/j.cnki.kzgc.2014.06.008.GUAN Z W, CHEN G C, XU Y F, YU J S.Short-term prediction model of wind power based on improved EMD and SVM[J].Control Engineering of China, 2014,21(6):833-837.doi:10.14107/j.cnki.kzgc.2014.06.008.
[13]MENG E H, HUANG S Z, HUANG Q, FANG W, WU L Z, WANG L.A robust method for non-stationary streamflow prediction based on improved EMD-SVM model[J].Journal of Hydrology, 2019(568):462-478.
[14]邰晓红,刘义.基于EEMD-PSO-SVM的月度CPI预测研究[J].统计与决策,2019,35(3):30-33.doi:10.13546/j.cnki.tjyjc.2019.03.007.TAI X H, LIU Y.Research on monthly CPI prediction based on EEMD-PSO-SVM[J].Control and Decision, 2019,35(3):30-33.doi:10.13546/j.cnki.tjyjc.2019.03.007.
[15]FAN G F, PENG L L, HONG W C, SUN F.Electric load forecasting by the SVR model with differential empirical mode decomposition and auto regression[J].Neurocomputing, 2016(173):958-970.
[16]TAO L, HE X G, RUI W.A hybrid LSSVM model with empirical mode decomposition and differential evolution for forecasting monthly precipitation[J].Journal of Hydrometeorology,2017(18):159-176.
[17]WANG S X,ZHANG N.Wind speed forecasting based on the hybrid ensemble empirical mode decomposition and GA-BP neural network method[J].Renewable Energy, 2016(94):629-636.
[18]王晓平,闫飞.基于神经网络分析的北京城镇农产品冷链物流需求预测[J].广东农业科学,2018,45(6):120-128.doi:10.16768/j.issn.1004-874X.2018.06.020.WANG X P, YAN F, Forecast of cold chain logistics demand for agricultural products in Beijing based on neural network[J].Guangdong Agricultural Sciences, 2018, 45(6):120-128.doi:10.16768/j.issn.1004-874X.2018.06.020.
[19]姜百臣,冯凯杰,彭思喜.基于改进持支向量机的猪肉价格预测研究[J].广东农业科学,2018,45(12): 158-164.doi:10.16768/j.issn.1004-874X.2018.12.026.JIANG B C, FENG K J, PENG S X.Research on pork price prediction based on improved support vector machine[J].Guangdong Agricultural Sciences, 2018,45(12):158-164.doi:10.16768/j.issn.1004-874X.2018.12.026.